Para lograr una gran fortuna, debemos recurrir a la magia del interés compuesto cuya fórmula es: Tú dinero por (1+i)^n, donde los beneficios (intereses) se van sumando al capital principal. ¿Pero qué es el interés compuesto , en qué consiste y cómo funciona en realidad?
Albert Einstein llamó a esta aparente simple fórmula «el mayor descubrimiento matemático de todos los tiempos.»
Lo único que te separa de tus objetivos financieros son cuatro variables que anteriormente denominamos los 4 pilares de la educación financiera:
- El dinero que ganas.
- El dinero que no gastas (ahorro)
- El interés que consigues por tu dinero.
- El tiempo (variable en función de la rentabilidad que obtenemos por nuestra inversión)
Por tanto, cuanto más dinero inviertas y antes comiences, antes cumplirás ciertos objetivos financieros.
Ya que las palabras no pueden describir adecuadamente la naturaleza mágica del interés compuesto, probemos con unos efectos visuales.
Así funciona la magia del interés compuesto.
Así es como una sola inversión de 1200 euros crece con el tiempo en cuatro escenarios distintos de vehículos de inversión y rentabilidad, siempre y cuando los intereses sean añadidos al capital principal.
| Cuenta de ahorros (0,5%) | Depósitos a plazo fijo (2%) | Mercado de valores(5%) | Mercado de valores (9%) | |
| Inversión Inicial | 1.200 | 1.200 | 1.200 | 1.200 |
| 5 años | 1.230 | 1.325 | 1.532 | 1.846 |
| 10 años | 1.261 | 1.463 | 1.955 | 2.841 |
| 15 años | 1.293 | 1.615 | 2.495 | 4.371 |
| 25 años | 1.359 | 1.969 | 4.064 | 10.348 |
| 30 años | 1.394 | 2.174 | 5.186 | 15.921 |
| 35 años | 1.429 | 2.400 | 6.619 | 24.497 |
| 40 años | 1.465 | 2.650 | 8.448 | 37.691 |
Como se puede ver, dejando simplemente los 1200 euros, podrían convertirse en casi 40.000 euros en 40 años. No sólo has ganado el interés, sino que has ganado el interés de los intereses añadidos al capital principal. Y todo lo que había que hacer era invertir tu primer sueldo y reinvertir las ganancias cada año.
Ahora vamos a probar lo que sucede si hacemos una pequeña reinversión anual, y en lugar de invertir únicamente 1.200 euros, invertimos todos los años 1.200 euros, que básicamente serían 100€ al mes.
| Cuenta de ahorros (0,5%) | Depósitos a plazo fijo (2%) | Mercado de valores (5%) | Mercado de valores (9%) | |
| Inversión Inicial | 1.200 | 1.200 | 1.200 | 1.200 |
| 5 años | 7.321 | 7.695 | 8.494 | 9.674 |
| 10 años | 13.596 | 14.865 | 17.803 | 22.713 |
| 15 años | 20.030 | 22.782 | 29.684 | 42.775 |
| 25 años | 33.390 | 41.174 | 64.200 | 121.136 |
| 30 años | 40.323 | 51.829 | 88.899 | 194.211 |
| 35 años | 47.432 | 63.593 | 120.423 | 306.646 |
| 40 años | 54.721 | 76.582 | 180.656 | 479.642 |
Invirtiendo 1.200 euros cada año, en 40 años obtenemos casi medio millón de euros. Para llegar a un millón de euros sólo hay que ahorrar 2.500 euros al año (208 euros al mes), y a un interés del 9% en 40 años tenemos el millón.
Cuando en Negocios1000 analizamos la cantidad de dinero que debías ahorrar para ganar tu primer millón a los 65 años, calculamos que si tenías 20, únicamente debías ahorrar cada mes 361€, pensando en un 6% de rentabilidad. Si comienzas a los 25 años, debías ahorrar 499€. Comprobábamos cómo la cantidad de ahorro necesaria para alcanzar un millón de euros a los 65 años, se incrementaba drásticamente a medida que pasaban los años.
(Ver: Aquí está la diferencia entre comenzar a ahorrar a los 25 y a los 35 años)
También podríamos seguir con la contribución de 1200 euros anuales del ejemplo anterior, pero mejorando las habilidades de inversión. Si eres capaz de mejorar la rentabilidad anual promedio del mercado de valores, el premio de un millón de euros es tuyo.
La mejor parte del interés compuesto es que funciona de la misma forma para todos, tanto si tienes 20 euros para invertir como si tienes 200.000 euros.
La historia del inventor del ajedrez
Existe una historia que no creo que sea real, pero que se pone de ejemplo para explicar la magia del interés compuesto. Es la historia del supuesto inventor del ajedrez.
El inventor fue a ver al emperador de China, y le enseñó su creación, el juego del ajedrez. El emperador quedó tan asombrado que quería aquel juego para él, por lo que le dijo al joven inventor que si le dejaba el juego, le concedería un deseo.
Y el inventor le pidió algo muy simple: le pidió un grano de arroz para la primera casilla del tablero, 2 granos para la segunda casilla, 4 granos para la tercera, 8 para la cuarta y que fuera así, doblando sucesivamente la cantidad en cada casilla hasta la última casilla del tablero.
El emperador aceptó rápidamente, pues consideró aquella petición muy modesta. Incluso tenía la sensación de haber engañado a aquel joven al quedarse con su invento por unos pocos granos de arroz.
Pero cuando el emperador se dispuso a pagar, y fue calculando los granos necesarios conforme aumentaban las casillas del tablero, descubrió que para rellenar las últimas 10 casillas del tablero, necesitaría 35 trillones de granos de arroz. En toda China no había arroz suficiente para pagarle al inventor. Entonces el emperador se sintió engañado y ordenó matar al inventor.
Si no crees que puedes convertirte en millonario con sólo los recursos que tienes en este momento, ten en cuenta esta historia.
La historia de Oseola McCarty de Mississippi.
Esta historia sí que es real. Oseola McCarty nació en Mississippi en 1908. Durante casi 75 años, vivía en la misma casa sencilla, lavando ropa ajena para ganarse la vida y poner todo el poco dinero que podía en cuentas de ahorro de los bancos locales.
En el verano de 1995, Oseola fue noticia nacional cuando ella donó 150.000 dólares a la Universidad del Sur de mississippi para establecer un fondo de becas. Pronto se supo que esta mujer había logrado reunir casi un cuarto de millón de dólares durante su vida.
El tiempo -una parte clave de la ecuación del interés compuesto- ayudó a convertir sus escasas inversiones en cientos de miles de dólares.
Después de su muerte en 1999, uno de sus banqueros dijo:
«El tiempo fue capaz de convertir incluso las modestas ganancias de sus primeras inversiones en cientos de miles de dólares. Si hubiéramos sido capaces de conseguir que invirtiera en renta variable, hubiera conseguido millones de dólares en lugar de miles.»
La cantidad que ahorramos y el horizonte de tiempo son sólo dos terceras partes de la ecuación de la capitalización compuesta. Oseola destacó en ambas. Pero le hizo pagar un precio por ignorar la tasa de retorno sobre sus inversiones.
Por lo general, cuanto más riesgo se está dispuesto a asumir (por ejemplo, invertir en acciones en lugar de bonos o depósitos a plazo fijo), mayor será tu rentabilidad potencial. Pero el riesgo es una palabra de seis letras que asusta a un montón de gente: son felices conformándose con menores retornos para evitarlo.
La independencia financiera está a sólo 4 variables de distancia. Así que empieza a ahorrar ahora tanto como sea posible, así como a invertir tanto como te sea posible, y conseguir tanto interés por tus inversiones como te sea posible. Porque cuanto más pronto empiece la maravilla del interés compuesto a trabajar para ti, más pronto podrás alcanzar tus metas financieras.
Este artículo es el primero de una serie de artículos que vamos a realizar sobre inversión una vez o un par de veces a la semana.

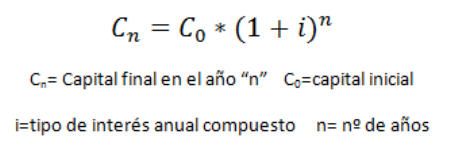
























6 comentarios